Full Html

Investigation of Structural, Thermal and Electronic Properties of Zincblende Indium Nitride using Local Density Approximation with Semi-core Pseudopotential

Zahid Usman ¹

 

1 Department of Physics, Division of Science and Technology, University of Education Lahore, Pakistan

Abstract

Density functional Semi-core pseudopotentials offer accurate calculations of the structural, thermal and electronic properties of zincblende InN within the context of local density approximation (LDA). Different structural parameters (the total energy per formula unit, equilibrium lattice constants, bulk modulus, bond length) and parameters defining the chemical reactivity of InN (Kohn Sham hardness and electronegativity) are calculated and compared with experimental data. Our calculated values of heat capacity at constant pressure (Cp), entropy (S) and enthalpy (H) at 298k and 1 atm pressure are 39.6 J/mole. K , 52 J/(mole.K), and -96.6 Kcal/m, which agree well with experimental values of 38.65 J/(mole.K), 43.5 J/(mole.K) and 109.7 Kcal/m, respectively. The electronic band structure calculations reveal the band gap of cubic InN to be 0.63 eV and the composition of band structure is well explained via the density of states. We observe s-d hybridization splits the Nitrogen 2-s band into two parts, one above and other below the In d-band with a large dispersion away from Brillouin zone, further splitting d-band into an inert doublet. Overall pattern and distribution of DOS is in good agreement with existing literature. Assuming the parabolic nature of valence and conduction bands, the effective mass theory has been implemented to calculate the effective masses of conduction electrons, holes and Luttinger parameters. These parameters dictate the scope of InN as a potential candidate in optoelectronic applications.

Keywords

Structural properties, Thermal properties, Effective mass theory, Spin ­polarization

INTRODUCTION

The group III-V nitrides have revolutionized the modern life. Aluminium Nitrides (AlN), Gallium Nitride (GaN), Indium Nitride (InN) and their alloys have shown their potential use in Optoelectronic devices, high power microwave transistors, lasers and light emitting diodes^1-4. The researchers are yet working enthusiastically to discover their application as chemical sensors^5-7 and in quantum cryptography⁸.These nitrides have direct bandgaps, greater thermal conductivities, high melting points and large bulk moduli. These properties are good enough to allure the scientists for manipulating these materials? in device fabrication. For example, for optical device application, it is unavoidable to go beyond the understanding of bandgap, in this scenario, we must have a sound knowledge of electron effective masses and valence band parameters so that we can analyze and interpret the experimental findings and predict their applications in advance. Among these nitrides, InN is least studied semiconductor due to the difficult growth of high-quality InN bulk samples⁹. The absence of good quality samples further obstructs the band-edge photoluminescence spectra, resulting in untrustworthy information about bandgap. Nevertheless, the bandgap of InN is calculated from absorption studies; therefore, the higher level of doping and poor quality of the crystal can lead to inaccurate measurement of energy bandgap. However, the development of better growth techniques like molecular beam epitaxy has provided a clear absorption edge through which an acceptable bandgap can be estimated. Recently Battacharya et al.¹⁰ have found InN bandgap to be 0.6 eV experimentally. Theoretical studies are now a days an efficient and economical tool to predict, understand and control the device characteristics with rapid pace. Frequent first principles studies have been performed for Group III-V nitrides over past few decades. Local density approximation (LDA)¹¹ has shared a greater part of such studies with pseudopotential plane wave basis set or with all electron method. It has been already proved that the LDA method encounters a significant underestimation of the band gap and binding energy in semiconductors^12-13. Hartree-Fock method has also been implemented but it is computationally more expensive and often overestimates the bandgap remarkably as compared to LDA. Like Ga 3d bands, LDA predicts the overlap of In 4d orbitals with N 2s bands, which has been nullified by the recent experiment performed for GaN. Therefore, it is expected that this might be true for InN too. In order to avoid this problem, self-consistent field interactions and screening effects are also included.¹⁴ Vogel et al.¹⁵ have corrected the bandgap value to be 1.3eV for Zincblende and 1.6 eV for wurtzite InN by taking into account the self-correction and relaxation effects. Van Schilfgaarde et al.¹⁶ have found these gaps to be 0.7 (ZB) and 0.8 eV for wurtzite InN using screened exchange potentials. GW method¹⁷ has shown a bandgap of only 0.01 eV for cubic InN. Su-Huai et al.¹⁸ have also carried out GW calculations and band gap of wurtzite InN is estimated to be 0.5 eV, while same calculations performed by Johnson and Ashcroft¹⁹ have predicted a band gap of 1.79 eV. Stampfl and Van de Walle²⁰ have used tight binding scheme to ensure the better convergence of Ga 3d, N 2p and In 4d potentials and have approximated a negative band gap of InN. This study aggravated the state of dilemma about the InN’s true band gap.

In this study, we have applied LDA method along with Semi-core potential (SCP) to explore the structural, thermodynamic and electronic properties of zincblende InN. Keeping in mind the importance of InN in device fabrication, we have also incorporated effective mass theory to get fruitful knowledge of effective masses of conduction electrons and holes.

SIMULATION DETAILS

DMole3 software²¹ has been used to investigate the structural, thermodynamic and electronic properties of zincblende InN using Local Density Approximation (LDA) method within density functional theory (DFT). The unit cell of zincblende InN contains two atoms whose shape is like a paralellopipe with same side lengths. The Zincblende InN belongs to F-43m where the Ga atoms are placed at the centre [0,0,0] and nitrogen atoms occupy a position (1/4, 1/4, 1/4) displaced from the centre. The length of three symmetric sides is 4.98 Å ²² and all three sides are inclined with each other at an angle of 60⁰. In order to get a more refined structure with lowest possible energy, we have performed geometry optimization. In this process, the lattice parameters obtained has been adjusted iteratively until and unless the structure obtains its lowest energy and where the force per atom approaches to zero. In order to treat the core electrons in InN, density functional Semi-core potentials (DSPPs) are implemented. These potentials reproduce accurate calculations due to the fact that these are obtained via fitting all-electron relativistic effects, containing non-local contribution and hence are norm conserving potentials²³ in nature. The relativistic effects become more significant, when the atomic numbers of the elements increase.

The atomic configurations of Indium and Nitrogen are 4d¹⁰5s²5p¹ and 2s²2p³ respectively for which the basis sets are expanded with a cut off energy of 3.5 Å. The other optimization parameters for total energy, maximum force per atom and maximum displacement are set to be 2.7e^-4 eV, 0.0544 eV/Å, and 0.005 Å respectively. The calculations for structural properties are accomplished with and without spin-polarization, and their comparative effect on atomic charge densities has been discussed through Mullikan charge analysis. Electronegativities and Kohn Sham hardness on InN are approximated using HOMO-LUMO calculations. We have performed vibrational analysis which is a key step to get important thermal properties like entropy, specific heat capacity at constant pressure and enthalpy of formation. A monkhorst mesh of 7*7*7 is used in k-space to calculate the electronic band structure properties in high symmetry directions. Assuming the shape of conduction band minimum (CBM) and valence band maximum to be parabolic, we have approximated the effective masses of conduction electrons and valence holes using effective mass theory. At the end Luttinger parameters are calculated on the basis of effective masses.

RESULTS AND DISCUSSION

Structural Properties

The geometry optimization of zincblende InN unit cell has resulted in a more refined structure with best possible lowest energy. The total energy is the sum of various type of energies like kinetic energy, electrostatic energy and exchange-correlation energy and is written as

1 ET(ρ)= T ρ+U ρ+EXC ρ

Where ET(ρ) represents the total energy depending upon charge density (ρ), T( ρ ), U( ρ ) and EXC(ρ) represent the kinetic energy of the non-interacting system of particle, electrostatic energy and exchange-correlation energy respectively. All these contributing energies are subsequently dependent upon charge density ρtoo  . Here, we are considering separate wave functions for spin up and spin down electrons, therefore total energy includes significant contribution from spin-polarization too. The total energy per formula unit is predicted to be 10.65eV after fitting the equation of state. The equilibrium lattice parameters for this geometrically optimized structure calculated with the help of LDA-SCP are found to be 4.935 Å. These lattice parameters are nearly 1.0% less than the experimental lattice parameters 4.98 Å. ²² Our calculated values of equilibrium lattice parameters are summarized in table 1 along with the experimental and previous first-principles calculations. This underestimation in lattice parameters is attributed to the typical nature of local density approximation which shows its weakness when the exchange correlation effects²⁴ are encountered. The table 1 also reveals that the measured value of lattice constant a is in accordance with the existing theoretical results^25-27 except those obtained through GGA (5.169 Å )²⁸.

Since the total energy includes the spin polarization term, which seriously affects the ionic properties of cubic InN, therefore, we have performed Mulliken population analysis for spin-polarized and non-spin-polarized InN systems. The outcome of this analysis results in atomic charge densities and In-N bond length, as presented in table 1. Our finding about the population analysis of InN reveals an important fact that the Indium (In) acts as a cation and the nitrogen as anions as evident from the net charge acquired by In and N in table 1. Mulliken population data table further signify the effect of spin polarization on the valence charges of atoms. Table 1 suggests that the, the ionicity of the structure would be reduced through the inclusion of spin polarization effect, which is further verified by the reduction of occupation number of s, p and d valence shells for In and N as apparent from table 1. A careful look at the change in the occupancy of p and d of both atoms reveals that the reduction in ionicity is more significant for Indium rather than nitrogen. This trend is in complete agreement with that of AlN as proposed by Eliseo Ruiz et al.²⁹ This means that polarization field permits more charge to be localized within In-N bonding regions.

The bond length for In-N is calculated to be 2.137 Å, which is slightly underestimated than the experimental value of 2.16 Å as measured by Jeff et al.³⁰ through the EXAFS measurements. Likewise, our calculated value of the bond length is in good agreement with that of well converged calculations by A.F. Wright³¹which is 2.04 Å. The bulk modulus can be predicted by a semi-empirical relation where the average distance between two neighbors is taken into account as proposed by Cohen et al.³²

2 B=1971-220λd3.5

Where λ is iconicity factor, whose value is 1 for group III-V nitrides and d represents the bond length between In and N.

The bulk modulus calculated through this formula is enlisted in table 1 along with other experiment³³ and well converged first principle studies^{26-28,3 4-35}. The table 1 shows that the bulk modulus calculated through LDA-Semicore potential is 123 GPa, extremely close with the experimental value of 125.5GPa³³ but underestimated as compared to the bulk modulus (156GPa) calculated via Birch Murnaghan equation of state. Our result for bulk modulus is in good agreement with well converged first principle studies of Tarun et al²⁸, whereas it is underestimated up to few percent from other theoretical reports^26-27,34,35. By and large, the bulk modulus reported herein shows good agreement with experiment and first principles calculations.

The electronegativity and Kohn Sham hardness are widely used concepts to determine the chemical reactivity of a material. Therefore, we have also calculated the HOMO-LUMO energy gaps, which are further used to calculate the Kohn Sham hardness and electronegativity by the following expressions³⁶.

Electronegativity:    χ=- (ε_HOMO- ε_LUMO)/2

Kohn Sham Hardness:      ζ= ε_LUMO - ε_HOMO

The corresponding values of HOMO-LUMO energies of zincblende InN calculated with LDA are -4.985 eV and -4.491 eV respectively. We have utilized these energies to calculate the electronegativity and Kohn Sham hardness respectively. The electronegativity has the value of 0.247eV while Kohn Sham hardness is 0.494 eV. It is evident from the HOMO-LUMO energies that the highest occupied Kohn-Sham orbital (HOMO) and LUMO orbitals lie very close to each other resulting in an energy gap of nearly 0.5 eV, while the electronegativity calculated through HOMO-LUMO energy gap is approximated to be 0.247 eV. This electronegativity in turns exhibits that more charge is localized around the nitrogen (N) atom. This further predicts that Nitrogen is stabilizing the electrons more than Indium. Energy band gap actually demonstrates the energy required to eject an electron from an ionic bond, therefore, a low energy gap suggests that the electrons can be easily ejected from the ionic bond.

 

 

 

Table 1: Lattice parameters a (Å), bulk modulus B (GPa), Valence charge of atoms (Q(In&N)) and bond Length d (Å). The orbital charges shown in braces are those calculated for non-spin polarized system and other values belong to spin polarized system.

Quantity	Present study	Experiment	Other calculations
a0	4.935	4.9822	4.80125, 4.92026, 4.94727, 5.16928
q(In)	0.877
5s	(1.261) 0.631
5p	(0.731) 0.371
5d	(0.122) 0.060
q(N)	-0.877
2s	(1.779) 0.890
3p	(4.083) 2.041
dIn-N	2.137	2.16030	2.0431
B	123	125.533	13735, 126.1428, 16126, 13927, 12134

 

Thermodynamic Properties

We have evaluated Hessian matrix to explore the important thermodynamic properties of zincblende InN. The vibrational analysis is performed, which provides a gist of knowledge about enthalpy (H), entropy (S) and heat capacity at constant pressure (C_p). These properties are obtained as a function of temperature as proposed by Hirano³⁷. In context of ideal gas approximation, the enthalpy (H) can be calculated as:

3 HT=Ev + Er + Etr + RT

Where the subscripts stand for vibrational, rotational and translational energies and R is a real gas constant at temperature T. Whereas, these contributing terms are calculated using the following equations:

4 Ev=  Rk12∑ihvi+RK ∑ihviexp(-hvi/kT)1-exp(-hvi/kT)

5 Etr =32RT

6 Er =RT

Here, the k is symbolic representation of Boltzman constant, h is plank’s constant and vi represents i^th vibrational frequencies. Similarly, the entropy is computed as:

7 Str=  52RlnT+32Rlnw-Rlnp-2.31482

8 Sr(linear)=  Rln8π2lkT σh2+R

9 Sr(nonlinear) = R2ln [ πσ8π2cIAh8π2cIBh                              8π2cICh(kThc)3 ]+32R

10 Sv  =  R∑ihvikTexp(-hvi/kT)1-exp(-hvi/kT)-R ∑iln(1-hviexp(-hvi/kT))

In above equations, w represents the molecular weight, I is the moment of inertia with subscript showing its directions along x, y and z-axis. The specific heat capacity at constant pressure (C_p) contains the various terms as follows:

11 Cvib=  R∑i(hvikT)2exp-hvikT1-exp-hvikT

12 Ctr =52RT

13 Cr(linear)=R

14 Cr(nonlinear)=32R

The specific heat capacity at constant pressure is calculated similarly against temperature and fig (1a) shows its comparison with experimental data ³⁸ and theoretical data ³⁹.

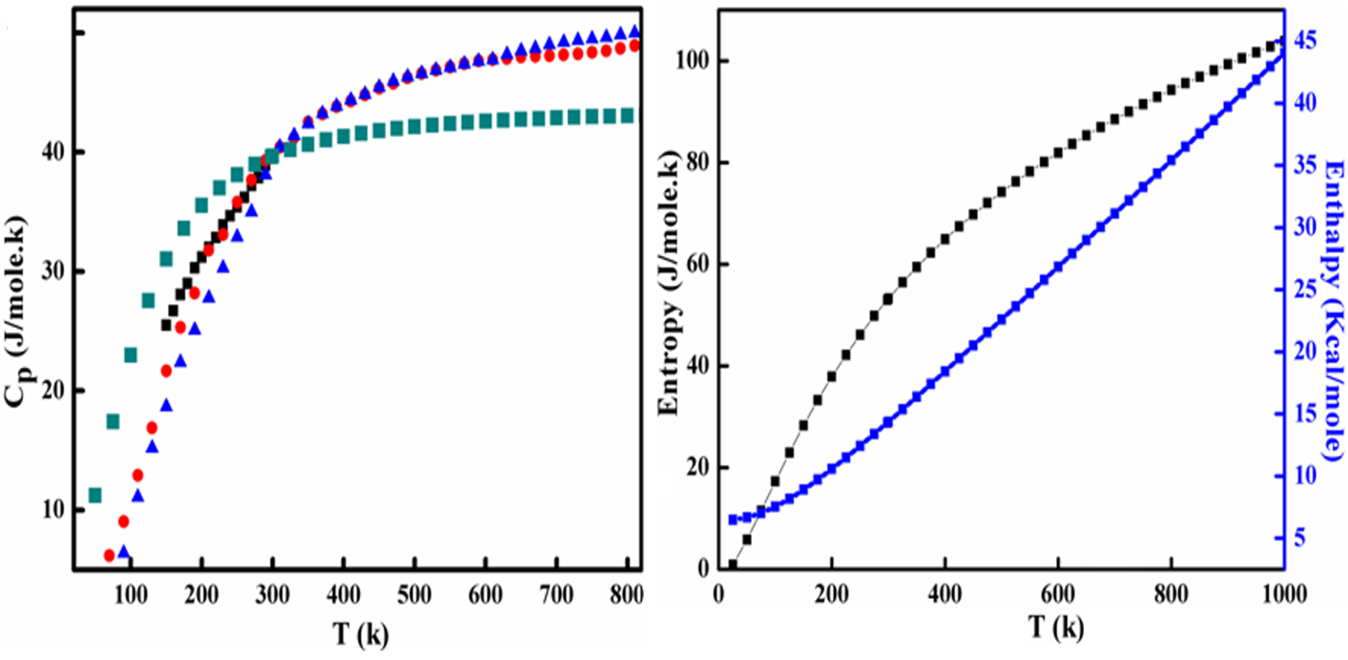
Figure 1: (a) The specific heat at constant pressure and (b) shows entropy and standard enthalpy as a function of temperature (K).

The experimental data on Cp (diamond shaped) in figure (1a) belongs to Krukowski et al.³⁸, where as the data in triangular and circular dotted line is that calculated by Onderka et al.³⁹ at high temperatures who used empirically extended Deby and Einstein heat capacity models for non magnetic crystalline systems and fit these models to the experimental data. Later on, he calculated the standard enthalpy by C_p/T integration. It is evident from figure (1a) that our calculated value of Cp (39.6J/(mole.K)) at standard temperature (298.16k) and pressure (1 atm) is in good agreement with experimental value of 38.65 J/(mole.K) calculated at 293k by Krukowski et al.³⁸ and heat capacity models of Onderka et al³⁹. These calculated values of entropy (S), and enthalpy (H) against temperature ranging from 0k to 1000k are calculated by using above formulae and are depicted in figure (1b). A comparison of the calculated values of S and H is presented along with already existing experimental data in Table 2.

 

Table 2: Specific heat capacity at constant pressure (J/(mole.K)), entropy (J/(mole.K)) and standard enthalpy (Kcal/mole).

Physical quantity	Present study	Experiment	Other calculations
Cp	39.6	38.6538	39.1039 42.0340
S	52.6	43.541	31.639
H	-96.6	-109.742, -129.343	-96.539

 

The entropy value in our case is 52 J/(mole.K), which is slightly overestimated as compared to the experimental value of 43.5⁴¹ as well as with that of Onderka et al.³⁹(31.6 J/(mole.K)). Kabaschewski⁴¹ calculated stand entropy to be 43.5 J/(mole.K). The standard enthalpy of formation in our case is -96.6 Kcal/mole, which lies near to the experimental values of -109.7 Kcal/mole and -129.3 Kcal/mole measured through Knudsen cell method^42,43. Analogous to the experimental results, our calculated value is in good agreement with theoretical value of -96.5 Kcal/mole calculated by Onderka et al.³⁹ in high temperature regime.

Electronic Properties

The calculated energy bandgap topology using LDA approach is consistent with typical zincblende InN band structure as reported in existing literature¹⁰ and is shown in Figure 2. The energy bandgap of InN is 0.63 eV, which is slighty overestimated than the experimental value of 0.6 eV suggested by Battacharya¹⁰ and 0.56 eV⁴⁴ proposed by Goldhahn et al.⁹ Unlike this, our computed bandgap value is much underestimated than 1.9eV proposed by Madelung et al.⁴⁵

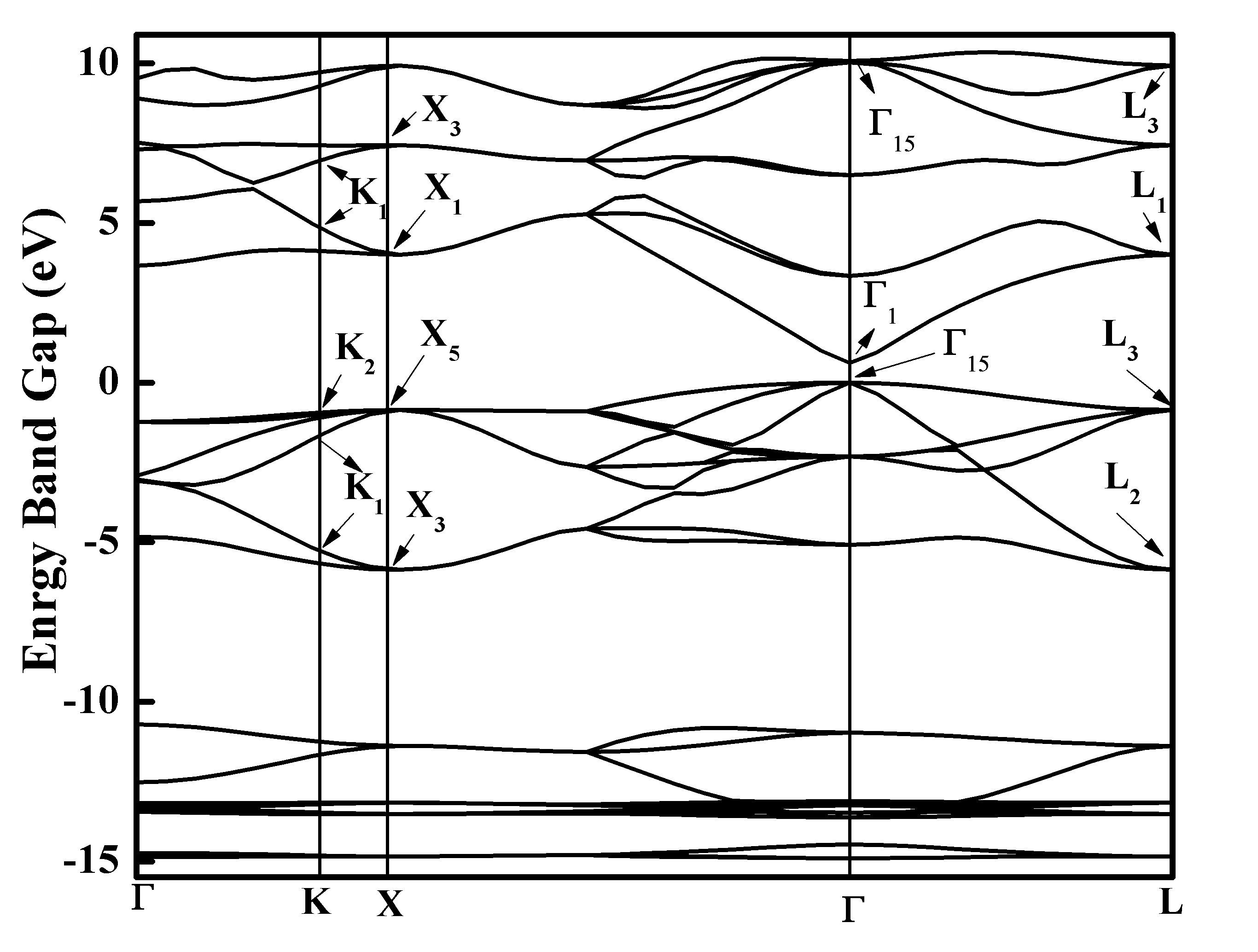
Figure 2: Band gap for zincblende InN

Our value is positive and shows better agreement with theoretical results except that of Stampfl et al.²⁰ whose bandgap is negative which is obtained through the evaluation of bandgap as a function of lattice parameters, subsequently extrapolated at equilibrium lattice parameters. The lowest valence band far from Fermi level is localized between -14.43 eV and -15.014 eV, and is composed of dominant s-states as evident from figure 3b. The vital contribution in this region is inherited by N-2s (Figure 3c) with a significant contribution from InN d- states too (Figure 3d). While the part played by N- p states, In-5s and 5p states is negligible in this region as apparent from Figure 3(c). The band structure (Figure 2) also reveals some sort of hybridization, which is due to In d-DOS (Figure 3d) and Nitrogen 2s-states, as apparent from figure 3 (c & d). The second valence band is located in between -13 eV and -10.7 eV, where the major contribution comes from In d-states as shown in Figure 3(d). A reasonable role is played by N s-states in this second lowest valence band, but the contribution from In 5-s and 5-p states is negligible. PDOS and Atomic DOS further explores, that the lower part of this band has only In d-states contribution, but upper part of this band around -11eV contains N 2-s and In 4-d hybridized states. This s-d hybridization splits the Nitrogen 2-s band into two parts, one above and other below the In d-band with a large dispersion away from Brillion zone centre as s-d mixing is prohibited at Gamma point, which is in accordance with same trend^47-49 observed in case of cubic GaN. Moreover, because of this hybridization, d band is also splitted to inert doublet which is in accordance with Ding et al.⁵⁰ The top valence band width is 5.6 eV, whose upper part is densely populated with N 2-p states, with a minor contribution performed by In 5-p states. Whereas the lower part of this valence band is comprised of In 5-s and N 2-p hybridized states as shown in Figure 3(c). This hybridization causes significant reduction in band gap of zincblende InN. Here we choose highest valence band to be at zero energy (Fermi level) at Gamma point, the band exactly above this valence band is termed as conduction band, which also resides at Gamma point. So the zincblende InN is a direct band gap structure. The partial DOS for cubic InN shows that the conduction band preserves dominant p-states character, where the s-states are reasonably lower as shown in Figure 3b. This p-character belongs to dominant In 5-p and reasonable N 2-p states. From Figure 3(c), In s and p-states show hybridization around 7eV. Surprisingly, the In d-states are also present in conduction band in between 3eV to 10eV. This pattern and distribution of DOS is in good agreement with first principles study of Tarun et al.²⁸

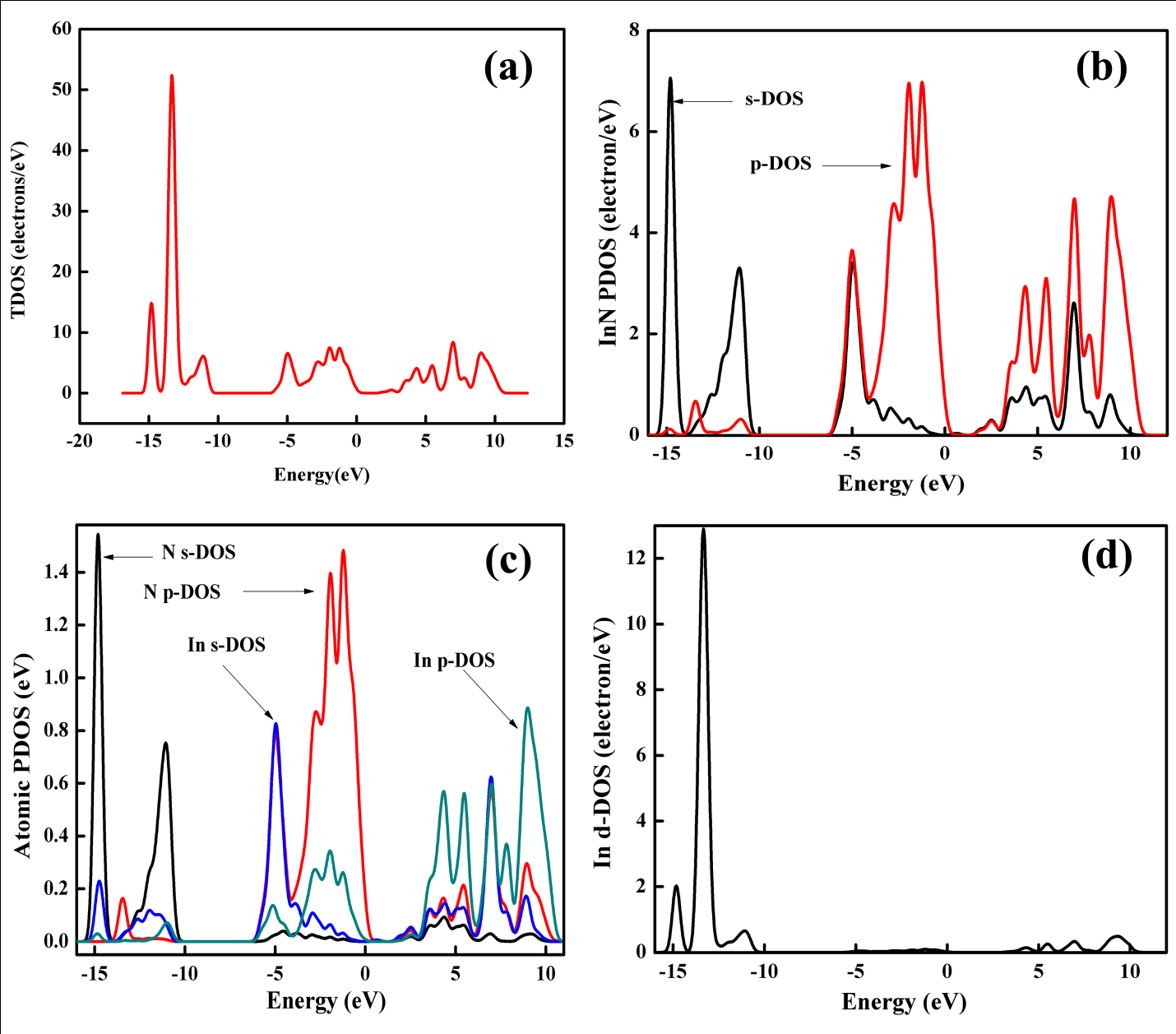
Figure 3: (a) Total DOS (b) InN partial DOS (c) Atomic DOS and (d) represents In-d DOS.

Generally, the effective mass theory is an excellent source to get useful information about the optical and transport properties of semiconductors near the band-edges. These two properties are linked with the electronic properties and hence with the electronic band structure directly. Therefore, we have implemented the effective mass theory to get a gist of electronic properties on the basis of electronic band structure of zincblende InN. The bandgap of cubic InN is direct, which guarantees excellent optical characteristics and superior electronic transport in conduction band. For instance, if we ignore the minute anisotropy of energy bands by assuming its parabolic nature, then the relation for electronic band-edge around conduction band is written as⁵¹.

15 ?Eck=Eg+?2k22m*

Where m^* is the effective mass of electron in conduction band, E_c(k) the energy of conduction band at a certain value of wave vector k and E_g represents the electronic energy gap. As, mostly in group III nitrides, topmost valence band is formed by p-type DOS. In p-state, an electron carries an angular momentum of h/2π, since electron have its inherited spin, and therefore, this spin is a way to interact the electron with its magnetic field, induced due to its orbital motion. Therefore, this spin orbit coupling severely affects the top of valence band and hence is important most to study. Since the zincblende structures shows cubic symmetry, that is why the crystal field splitting is absent in cubic structures. The spin orbit interaction lifts the degeneracy with a four-fold and two-fold degeneracy. The top of valence band contains four fold degenerate states comprising of two heavy holes (hh) and two light holes (lh), whereas the remaining two bands are called split-off (SO) bands. It is worth mentioning here that the optical transport is strongly dependent upon hole states, which are represented by angular momentum states. To evaluate valence band structure, we have used the effective mass Hamiltonian using K.P theory⁵². The 6x6 k.p matrix for cubic crystal structures is written as

 

Whereas,

16 ?Q=-?22mo [ (γ1+γ2) (kx2+ky2) +(γ1-γ2) kz2]

17 ?T=-?22mo [ (γ1+γ2) (kx2+ky2) +(γ1+γ2) kz2]

18 ?S=i?2m03   γ3kx-ikykz

19 ?R=-?22m03   γ2 kx2-ky2-2i γ3 kxky 

Here the γ₁, γ₂ and γ₃ represent the Luttinger parameters, and m₀ is the free electron mass.

The effective masses for holes are calculated by fitting a parabola to the following E vs K curves respectively in the immediate vicinity (0.5%) of Γ-point in ΓX, ΓK and ΓL directions:

20 ?Ehh=?2k22mhh

21 ?Elh=?2k22mlh

22 ?Eso=-?ESo-?2k22mlh

 where, E_hh, E_lh and E_so represent the energies of heavy hole, light hole and spin orbit split- off hole energy.

The parabolic fits for conduction band, topmost valence band and second parabola are shown in Figure 4.

The conduction band fit, topmost valence band fit and the second highest band fit contribute the effective masses for conduction electrons, heavy holes, and light holes respectively. The parabolic fit in Figure 4 is depicted by lines with markers.The calculated effective masses for these holes are calculated and summarized in table 3. It is worth mentioning that split off hole is isotropic and hence is independent of k direction. In order to calculate Luttinger parameters, we have solved the above given matrix by excluding the non-parabolic terms at a certain value of the wave vector (k). The evaluation of this matrix leads to three expressions in high symmetry directions, linking effective masses with Luttinger parameter^53-54.

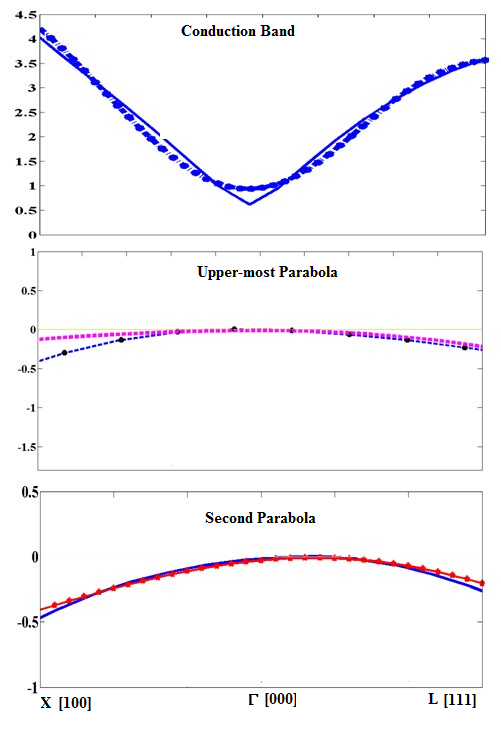
Figure 5: (a) The parabolic fits to the conduction band (b) the highest occupied valence band and (c) second topmost valence band.

These equations are

23 γ1=12[mlh-1 100+mhh-1 100]

24 γ2=14[mlh-1 100-mhh-1 100]

25 γ3=14[mlh-1 111-mhh-1 111]

The calculated effective masses are incorporated into these equations and the Luttinger parameters are obtained, which are also written in Table 3.

 

Table 3: The calculated effective masses in units of electron mass (m₀)

Ref	m*	mhh [100]	mhh [111]	mhh [110]	mlh [100]	mlh [111]	mlh [110]	mso
This study	0.15	2.394	2.796	3.382	0.29	0.23	0.379	0.33
Ref 55	0.13	1.18	2.89	2.12	0.21	0.19	0.2	0.36
Ref 55	0.10	2.18	2.29	3.10	0.89	0.93	0.79	0.30
Ref 55	0.12	0.83	0.83	1.55	0.16	0.16	0.15	0.30

 

Table 4: Luttinger parameters ( γi ) for zincblende InN calculated from Effective masses of holes.

Paramter	This work	Ref 55	Ref 57	Ref 58
γ1	1.933	3.27	2.78	6.817
γ2	1.515	1.26	0.97	2.810
γ3	1.54	1.63	1.22	3.121

 

The effective masses calculated in our case for heavy hole, split-off hole and conduction electron are in good agreement with Tadjer et al.⁵⁶, but the masses for the light hole are fairly underestimated. On the average, the effective masses calculated by us using LDA-Semicore potential are in good agreement with other first principle studies mostly performed with empirical pseudopotential approach. Our results for Luttinger parameters lie very close to that of FPLAPW method⁵⁵ or by empirical method⁵⁷ but good agreement does not exist as far as the results of GW-optimized effective potential method⁵⁸ is concerned, where the band gap has been observed to be negative.

CONCLUSIONS

The structural, thermodynamic and electronic properties of zincblende InN are explored in the perspective of density functional theory (DFT) using Local Density Approximation (LDA) method along with Semicore pseudopotential. The total energy per formula unit is calculated to be 10.65eV, whereas the equilibrium lattice constants are approximated to be 4.935 Å nearly 1.0% less than the experimental lattice parameters 4.98 Å. We have performed Mulliken population analysis for spin-polarized and non-spin-polarized InN systems to evaluate the effect of spin-polarization on orbital charge density. The population analysis of InN verifies the cationic nature of Indium (In) and anionic nature of nitrogen atoms as shown by the net charge acquired by In and N, where the reduction of occupation number of s, p and d valence shells for In and N happens. Ionicity of Indium atom reduces significantly as compared to nitrogen. The polarization field is actually permitting more charge to be localized within In-N bonding region. The bond length for In-N is calculated to be 2.137 Å, which is slightly underestimated than the experimental value of 2.16 Å as measured by Jeff et al. through the EXAFS measurements. The bulk modulus predicted by a semi-empirical relation as proposed by Cohen et al. is 123 GPa concurrent with the experimental value of 125.5GPa. HOMO-LUMO energy gaps calculations are carried out to calculate the Kohn Sham hardness and electronegativity of InN unitcell. A smaller HOMO-LUMO gap (0.5 eV) depicts that the electrons can be easily ejected from the ionic bond. The Vibrational analysis is performed to calculate enthalpy (H), entropy (S), and heat capacity at constant pressure (Cp) as suggested by Hirano. Our calculated value of Cp at room temperature and 1 atm pressure is 39.6J/(mole.K) , which agrees well with experimental value of 38.65 J/(mole.K) calculated at 293k by Krukowski et al .The entropy value in our case is 52 J/(mole.K), which is slightly overestimated as compared to the experimental value of 43.5 J/9mole.K). The standard enthalpy of formation in our case is -96.6Kcal/mole, which lies near to the experimental values of -109.7 Kcal/mole and -129.3 Kcal/mole measured through Knudsen cell method. Our calculated values of specific heat capacity at constant pressure, entropy and enthalpy are in good agreement with theoretical results. The electronic studies of zincblende InN show that its energy band gap is 0.63 eV, which is slightly overestimated than the experimental value of 0.6 eV.The topology of bandgap is same as observed in different well-known first principle studies. PDOS and Atomic DOS further explores, that the lower part of InN bandgap has only In d-states contribution, but upper part of this band contains N 2-s and In 4-d hybridized states. This s-d hybridization splits the Nitrogen 2-s band into two parts, one above and other below the In d-band with a large dispersion away from Brillion zone centre as s-d mixing is prohibited at Gamma point, which is in accordance with same the previous studies for cubic GaN. This hybridization further splits d band into inert doublet which is in accordance with Ding et al. studies. Overall the pattern and distribution of DOS in our case is in good agreement with first principles study of Tarun et al. The effective mass theory has been implemented to calculate the effective masses of the electrons and holes. Our calculated effective masses for heavy and ligt holes are in good agreement with those calculated through empirical methods. We have obtained the Luttinger parameters based on the calculated effective masses. By and large, our results for Luttinger parameters are in accordance with the existing literature.1

References

1. Strite, S. . 1992. GaN, AlN, and InN: A review. Journal of Vacuum Science & Technology B: Microelectronics and Nanometer Structures 10:1237.

2. Morkoç, H., Strite, S., Gao, G. B., Lin, M. E., Sverdlov, B. & Burns, M. . 1994. Large?band?gap SiC, III?V nitride, and II?VI ZnSe?based semiconductor device technologies. Journal of Applied Physics 76:1363–1398.

3. Ponce, F. A. & Bour, D. P. . 1997. Nitride-based semiconductors for blue and green light-emitting devices. Nature 386:351–359.

4. Nakamura, Shuji . 1997. III–V nitride based light-emitting devices. Solid State Communications 102:237–248.

5. Nakamura, Shuji, Mukai, Takashi & Senoh, Masayuki . 1994. Candela?class high?brightness InGaN/AlGaN double?heterostructure blue?light?emitting diodes. Applied Physics Letters 64:1687–1689.

6. Nakamura, Shuji, Senoh, Masayuki, Iwasa, Naruhito, Nagahama, Shin-ichi, Yamada, Takao & Mukai, Takashi . 1995. Superbright Green InGaN Single-Quantum-Well-Structure Light-Emitting Diodes. Japanese Journal of Applied Physics 34:L1332.

7. Nakamura, Shuji, Senoh, Masayuki, Nagahama, Shin-ichi, Iwasa, Naruhito, Yamada, Takao, Matsushita, Toshio, Hiroyuki Kiyoku, Hiroyuki Kiyoku & Yasunobu Sugimoto, Yasunobu Sugimoto . 1996. InGaN-Based Multi-Quantum-Well-Structure Laser Diodes. Japanese Journal of Applied Physics 35:L74.

8. Nakamura, Shuji, Senoh, Masayuki, Nagahama, Shin-ichi, Iwasa, Naruhito, Yamada, Takao, Matsushita, Toshio, Kiyoku, Hiroyuki, Sugimoto, Yasunobu, Kozaki, Tokuya, Umemoto, Hitoshi, Sano, Masahiko & Chocho, Kazuyuki . 1998. Present status of InGaN/GaN/AlGaN-based laser diodes. Journal of Crystal Growth 189-190:820–825.

9. Nakamura, Shuji & Fasol, Gerhard . 1997. GaN Growth. In: The Blue Laser Diode. (pp. 35-77) 10.1007/978-3-662-03462-0_4

10. Bhattacharyya, Jayeeta, Ghosh, Sandip, Gokhale, M. R., Arora, B. M., Lu, Hai & Schaff, W. J. . 2006. Polarized photoluminescence and absorption in A-plane InN films. Applied Physics Letters 89:151910.

11. Perdew, J. P. & Zunger, Alex . 1981. Self-interaction correction to density-functional approximations for many-electron systems. Physical Review B 23:5048–5079.

12. Perdew, John P. & Levy, Mel . 1983. Physical Content of the Exact Kohn-Sham Orbital Energies: Band Gaps and Derivative Discontinuities. Physical Review Letters 51:1884–1887.

13. Sham, L. J. & Schlüter, M. . 1983. Density-Functional Theory of the Energy Gap. Physical Review Letters 51:1888–1891.

14. Lambrecht, W. R. L., Segall, B., Strite, S., Martin, G., Agarwal, A., Morkoç, H. & Rockett, A. . 1994. X-ray photoelectron spectroscopy and theory of the valence band and semicore Ga 3d states in GaN. Physical Review B 50:14155–14160.

15. Vogel, Dirk, Krüger, Peter & Pollmann, Johannes . 1997. Structural and electronic properties of group-III nitrides. Physical Review B 55:12836–12839.

16. van Schilfgaarde, M., Sher, A. & Chen, A. B. . 1997. Theory of AlN, GaN, InN and their alloys. Journal of Crystal Growth 178:8–31.

17. Kotani, Takao & van Schilfgaarde, Mark . 2002. All-electron GW approximation with the mixed basis expansion based on the full-potential LMTO method. Solid State Communications 121:461–465.

18. Wei, Su-Huai, Nie, Xiliang, Batyrev, Iskander G. & Zhang, S. B. . 2003. Breakdown of the band-gap-common-cation rule: The origin of the small bandgap of InN. Physical Review B 67(16).

19. Johnson, Kurt A. & Ashcroft, N. W. . 1998. Corrections to density-functional theory band gaps. Physical Review B 58:15548–15556.

20. Stampfl, C. & Van de Walle, C. G. . 1999. Density-functional calculations for III-V nitrides using the local-density approximation and the generalized gradient approximation. Physical Review B 59:5521–5535.

21. Delley, B. . 1990. An all?electron numerical method for solving the local density functional for polyatomic molecules. The Journal of Chemical Physics 92:508–517.

22. Trampert, A., Brandt, O. & Ploog, K. H. . 1997. Chapter 7 Crystal Structure of Group III Nitrides. Semiconductors and Semimetals 167–192.

23. Delley, B. . 2002. Hardness conserving semilocal pseudopotentials. Physical Review B 66.

24. Singh, David J. . 1994. Introduction to the LAPW Method. Planewaves, Pseudopotentials and the LAPW Method 35–43.

25. Wang, S. Q. & Ye, H. Q. . 2002. A plane-wave pseudopotential study on III V zinc-blende and wurtzite semiconductors under pressure. Journal of Physics: Condensed Matter 14:9579–9587.

26. Kim, Kwiseon, Lambrecht, Walter R. L. & Segall, Benjamin . 1996. Elastic constants and related properties of tetrahedrally bonded BN, AlN, GaN, and InN. Physical Review B 53:16310–16326.

27. Kanoun, M. B., Merad, A. E., Merad, G., Cibert, J. & Aourag, H. . 2004. Prediction study of elastic properties under pressure effect for zincblende BN, AlN, GaN and InN. Solid-State Electronics 48:1601–1606.

28. Maurya, Tarun K., Kumar, S. & Auluck, S. . 2010. Ab-initio study of electronic and optical properties of InN in wurtzite and cubic phases. Optics Communications 283:4655–4661.

29. Ruiz, Eliseo, Alvarez, Santiago & Alemany, Pere . 1994. Electronic structure and properties of AlN. Physical Review B 49:7115–7123.

30. Wright, A. F. . 1997. Elastic properties of zinc-blende and wurtzite AlN, GaN, and InN. Journal of Applied Physics 82:2833–2839.

31. Jeffs, N. J., Blant, A. V., Cheng, T. S., Foxon, C. T., Bailey, C., Harrison, P. G., Mosselmans, J. F. W. & Dent, A. J. . 1998. Exafs Studies of Group III-Nitrides. MRS Proceedings 512.

32. Cohen, Marvin L. . 1985. Calculation of bulk moduli of diamond and zinc-blende solids. Physical Review B 32:7988–7991.

33. Ueno, Masaki, Yoshida, Minoru, Onodera, Akifumi, Shimomura, Osamu & Takemura, Kenichi . 1994. Stability of the wurtzite-type structure under high pressure: GaN and InN. Physical Review B 49:14–21.

34. Briki, M., Zaoui, A., Boutaiba, F. & Ferhat, M. . 2007. Route to a correct description of the fundamental properties of cubic InN. Applied Physics Letters 91:182105.

35. Christensen, N. E. & Gorczyca, I. . 1994. Optical and structural properties of III-V nitrides under pressure. Physical Review B 50:4397–4415.

36. Zhan, Chang-Guo, Nichols, Jeffrey A. & Dixon, David A. . 2003. Ionization Potential, Electron Affinity, Electronegativity, Hardness, and Electron Excitation Energy:  Molecular Properties from Density Functional Theory Orbital Energies. The Journal of Physical Chemistry A 107:4184–4195.

37. 2002. Manual on Presentation of Data and Control Chart Analysis. (Seventh Edition). (pp. 5-37) ASTM International 10.1520/mnl10799m

38. Krukowski, S., Witek, A., Adamczyk, J., Jun, J., Bockowski, M., Grzegory, I., Lucznik, B., Nowak, G., Wróblewski, M., Presz, A., Gierlotka, S., Stelmach, S., Palosz, B., Porowski, S. & Zinn, P. . 1998. Thermal properties of indium nitride. Journal of Physics and Chemistry of Solids 59:289–295.

39. Onderka, B., Unland, J. & Schmid-Fetzer, R. . 2002. Thermodynamics and phase stability in the In–N system. Journal of Materials Research 17:3065–3083.

40. Slack, Glen A., Tanzilli, R. A., Pohl, R. O. & Vandersande, J. W. . 1987. The intrinsic thermal conductivity of AIN. Journal of Physics and Chemistry of Solids 48:641–647.

41. Edwards, Jimmie G. . 1994. Review of Materials Thermochemistry, by O. Kubaschewski, C. B. Alcock and P. J. Pergamon Spencer. The Journal of Chemical Thermodynamics 26:223–224.

42. Guryanov, I. A., Vlasov, G. P., Lesina, E. A., Kiselev, A. V., Baranov, V. S., Avdeeva, E. V. & Vorob?ev, V. I. . 2005. Cationic oligopeptides modified with lipophilic fragments: Use for DNA delivery to cells. Russian Journal of Bioorganic Chemistry 31:18–26.

43. Guryanov, I. A., Vlasov, G. P., Lesina, E. A., Kiselev, A. V., Baranov, V. S., Avdeeva, E. V. & Vorob?ev, V. I. . 2005. Cationic oligopeptides modified with lipophilic fragments: Use for DNA delivery to cells. Russian Journal of Bioorganic Chemistry 31:18–26.

44. Goldhahn, R., Schley, P. & Roppischer, M. . 2009. Ellipsometry of InN and Related Alloys. Indium Nitride and Related Alloys 315–375.

45. Stephenson, A. . 1983. Landolt -- Bornstein -- Numerical Data and Functional Relationships in Science and Technology. New Series Group V, Vol. 1, Physical Properties of Rocks . (Vol. 1) Springer-Verlag 10.1093/gji/74.2.644

46. Furthmüller, J., Hahn, P. H., Fuchs, F. & Bechstedt, F. . 2005. Band structures and optical spectra of InN polymorphs: Influence of quasiparticle and excitonic effects. Physical Review B 72.

47. Rinke, P., Scheffler, M., Qteish, A., Winkelnkemper, M., Bimberg, D. & Neugebauer, J. . 2006. Band gap and band parameters of InN and GaN from quasiparticle energy calculations based on exact-exchange density-functional theory. Applied Physics Letters 89:161919.

48. Fiorentini, Vincenzo, Methfessel, Michael & Scheffler, Matthias . 1993. Electronic and structural properties of GaN by the full-potential linear muffin-tin orbitals method: The role of the d electrons. Physical Review B 47:13353–13362.

49. Usman, Zahid, Cao, Chuanbao, Nabi, Ghulam, Kun, Dou Yan, Khan, Waheed S., Mehmood, Tariq & Hussain, Sajad . 2011. First-Principle Electronic, Elastic, and Optical Study of Cubic Gallium Nitride. The Journal of Physical Chemistry A 115:6622–6628.

50. Ding, S. A., Neuhold, G., Weaver, J. H., Häberle, P., Horn, K., Brandt, O., Yang, H. & Ploog, K. . 1996. Electronic structure of cubic gallium nitride films grown on GaAs. Journal of Vacuum Science & Technology A: Vacuum, Surfaces, and Films 14:819–824.

51. Suzuki, Masakatsu, Uenoyama, Takeshi & Yanase, Akira . 1995. First-principles calculations of effective-mass parameters of AlN and GaN. Physical Review B 52:8132–8139.

52. Luttinger, J. M. & Kohn, W. . 1955. Motion of Electrons and Holes in Perturbed Periodic Fields. Physical Review 97:869–883.

53. Enderlein, Rolf & Horing, Norman J. . 1997. Fundamentals of Semiconductor Physics and Devices. 10.1142/2866

54. Rosa, A. L., Scolfaro, L. M. R., Enderlein, R., Sipahi, G. M. & Leite, J. R. . 1998. p-type δ-doping quantum wells and superlattices in Si: Self-consistent hole potentials and band structures. Physical Review B 58:15675–15687.

55. Fritsch, Daniel, Schmidt, Heidemarie & Grundmann, Marius . 2003. Band-structure pseudopotential calculation of zinc-blende and wurtzite AlN, GaN, and InN. Physical Review B 67.

56. Tadjer, A., Abbar, B., Rezki, M., Aourag, H. & Certier, M. . 1999. Electronic properties and strain effects in zinc blende GaN and InN. Journal of Physics and Chemistry of Solids 60:419–424.

57. Vurgaftman, I., Meyer, J. R. & Ram-Mohan, L. R. . 2001. Band parameters for III–V compound semiconductors and their alloys. Journal of Applied Physics 89:5815–5875.

58. Rinke, Patrick, Winkelnkemper, M., Qteish, A., Bimberg, D., Neugebauer, J. & Scheffler, M. . 2008. Consistent set of band parameters for the group-III nitrides AlN, GaN, and InN. Physical Review B 77.